[10000印刷√] 三角形 二等分線 書き方 119273-三角形 二��分線 書き方
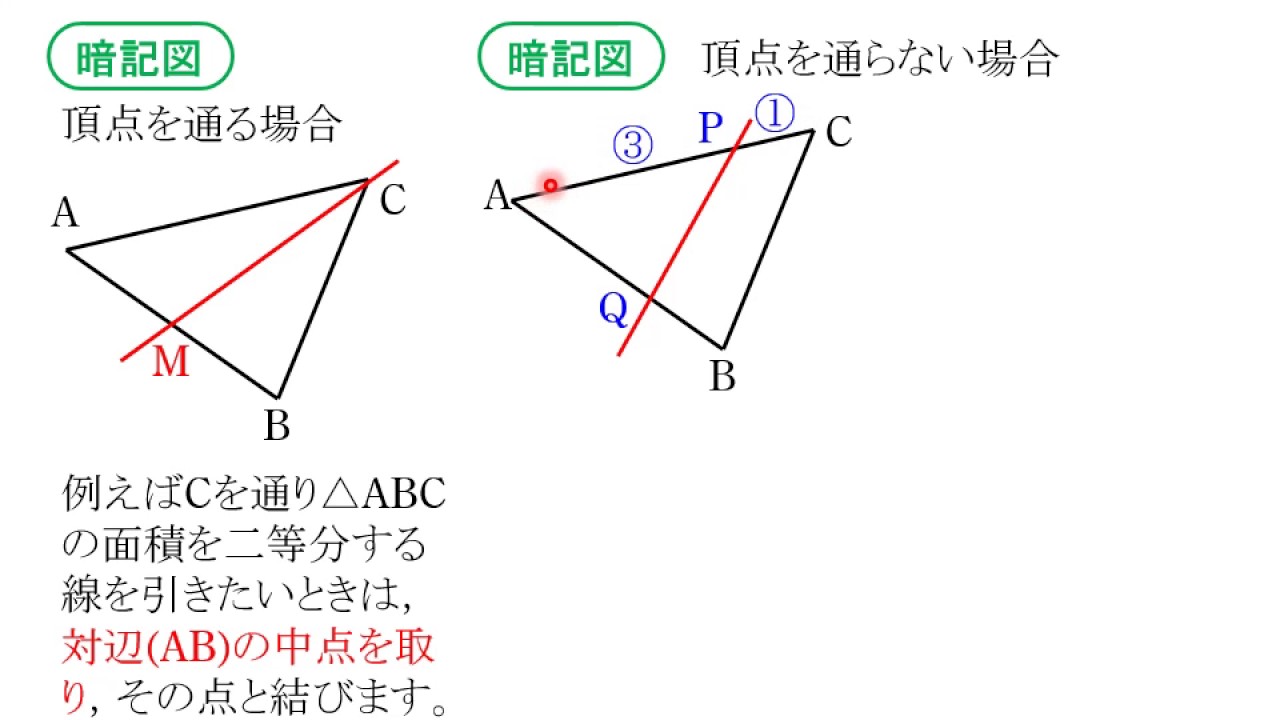
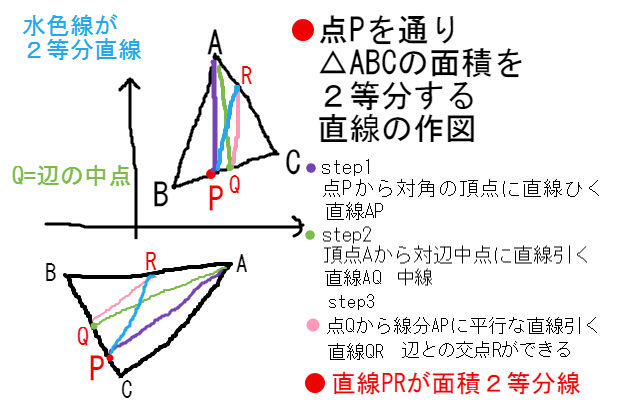
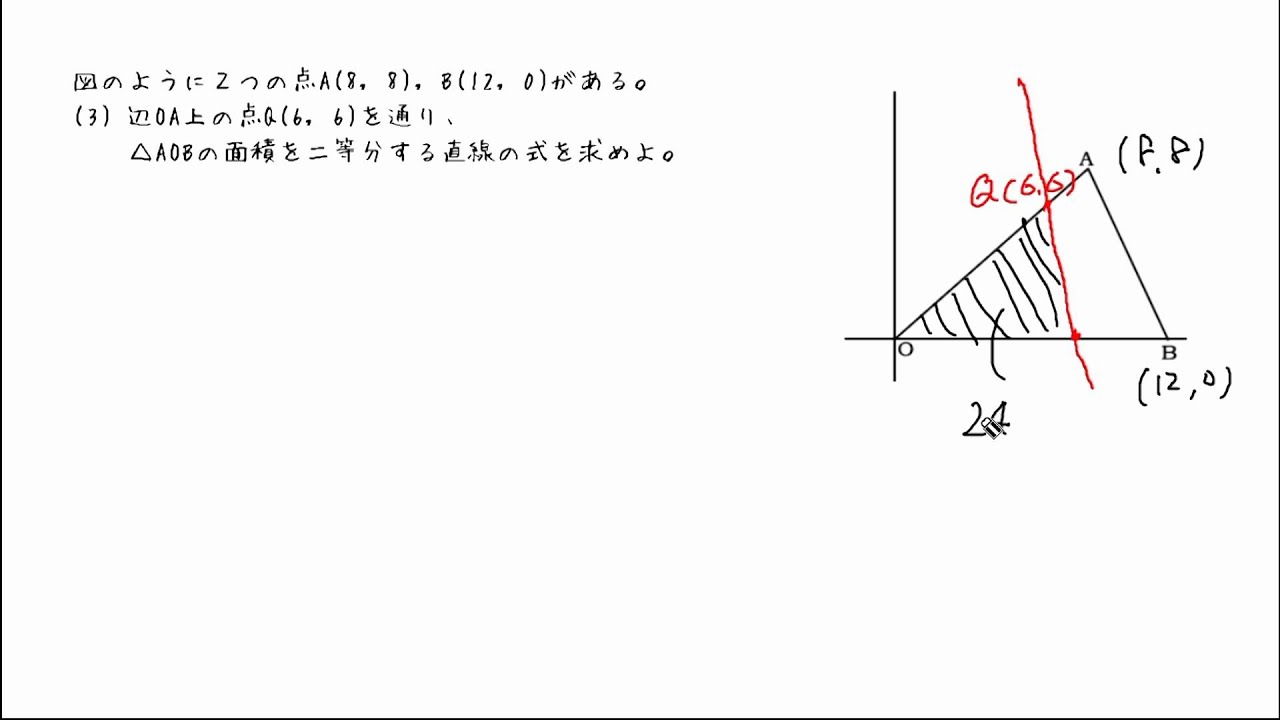
関数12 三角形の面積の二等分 Youtube
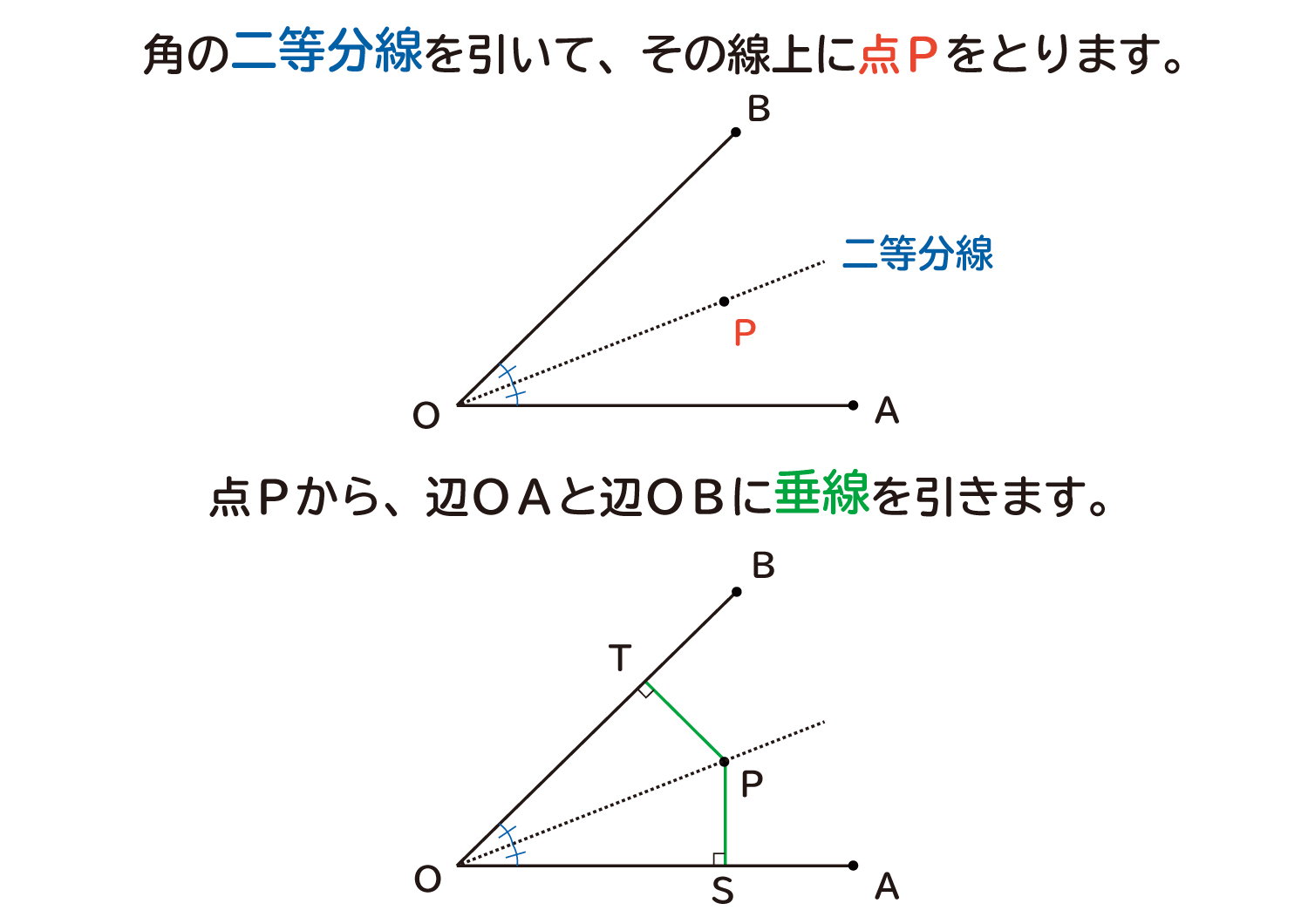
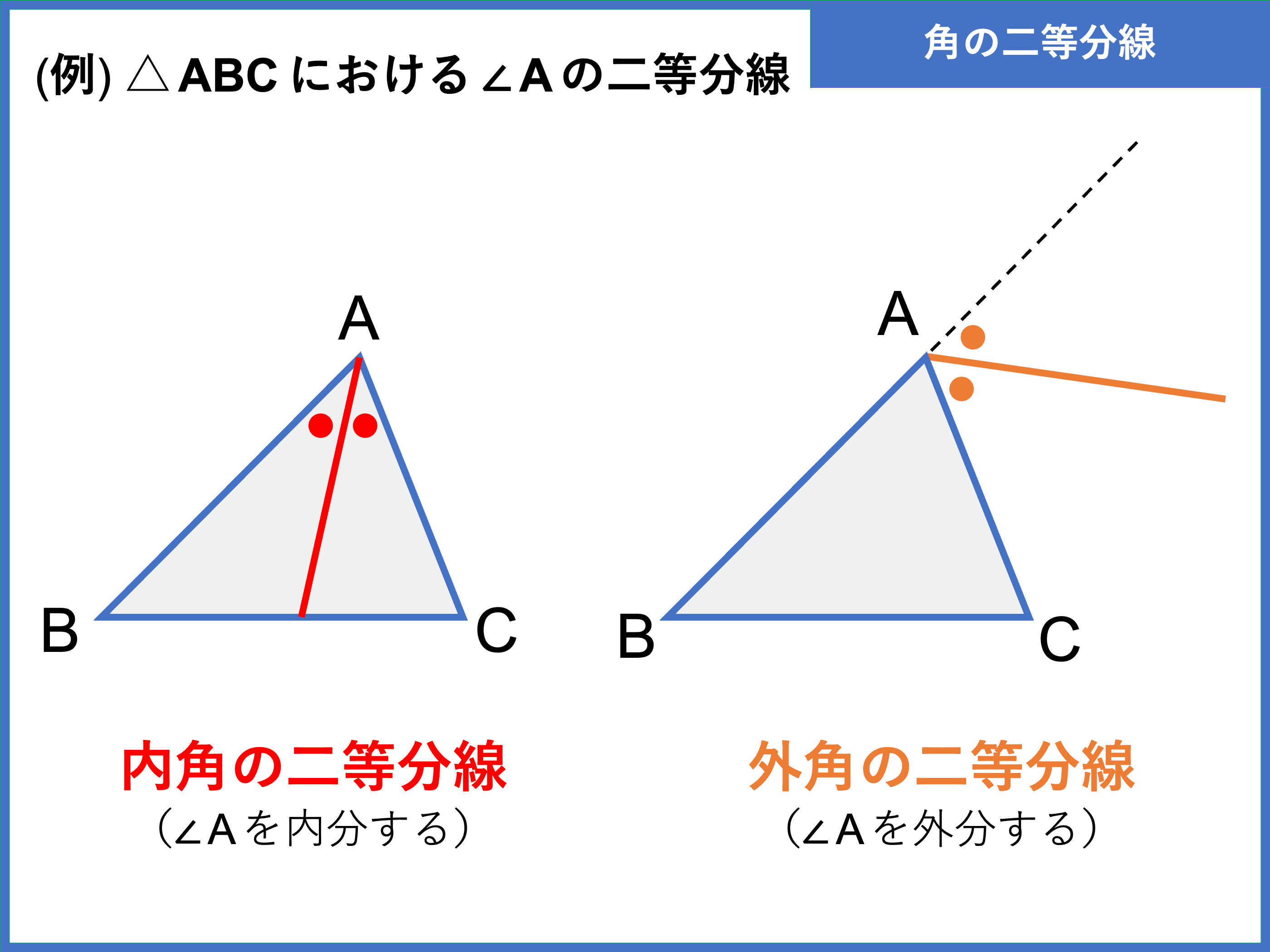
二等辺三角形の証明のまとめ ・(証明以外で)二等辺三角形がある時 底角が等しいことを使う 頂角の二等分線を引く→底辺を垂直に二等分する 90°ができる 底辺との交点が、底辺の中点となる ・二等辺三角形の証明 合同な三角形でなく角を利用 こんにちは、ウチダです。 今日は、中学1年生及び中学3年生で習う 「角の二等分線」 について、まずは作図方法(書き方)とそれが正しいことの証明を学び、次に角の二等分線と辺の比の定理(性質)を学びます。 また、記事の後半では、外角に関する問題
三角形 二等分線 書き方
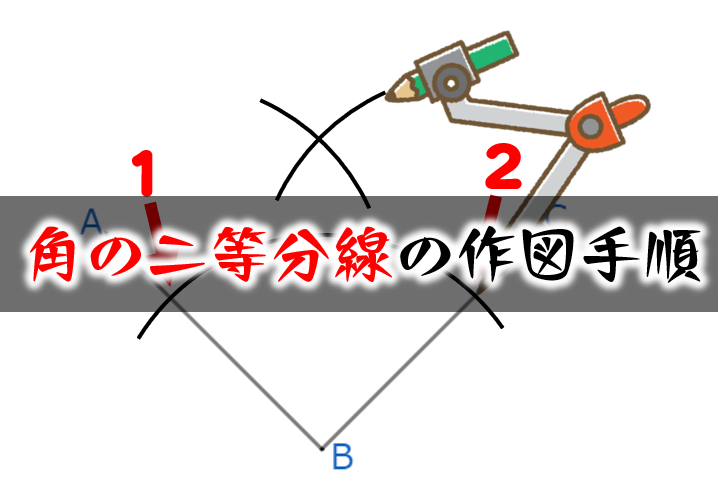
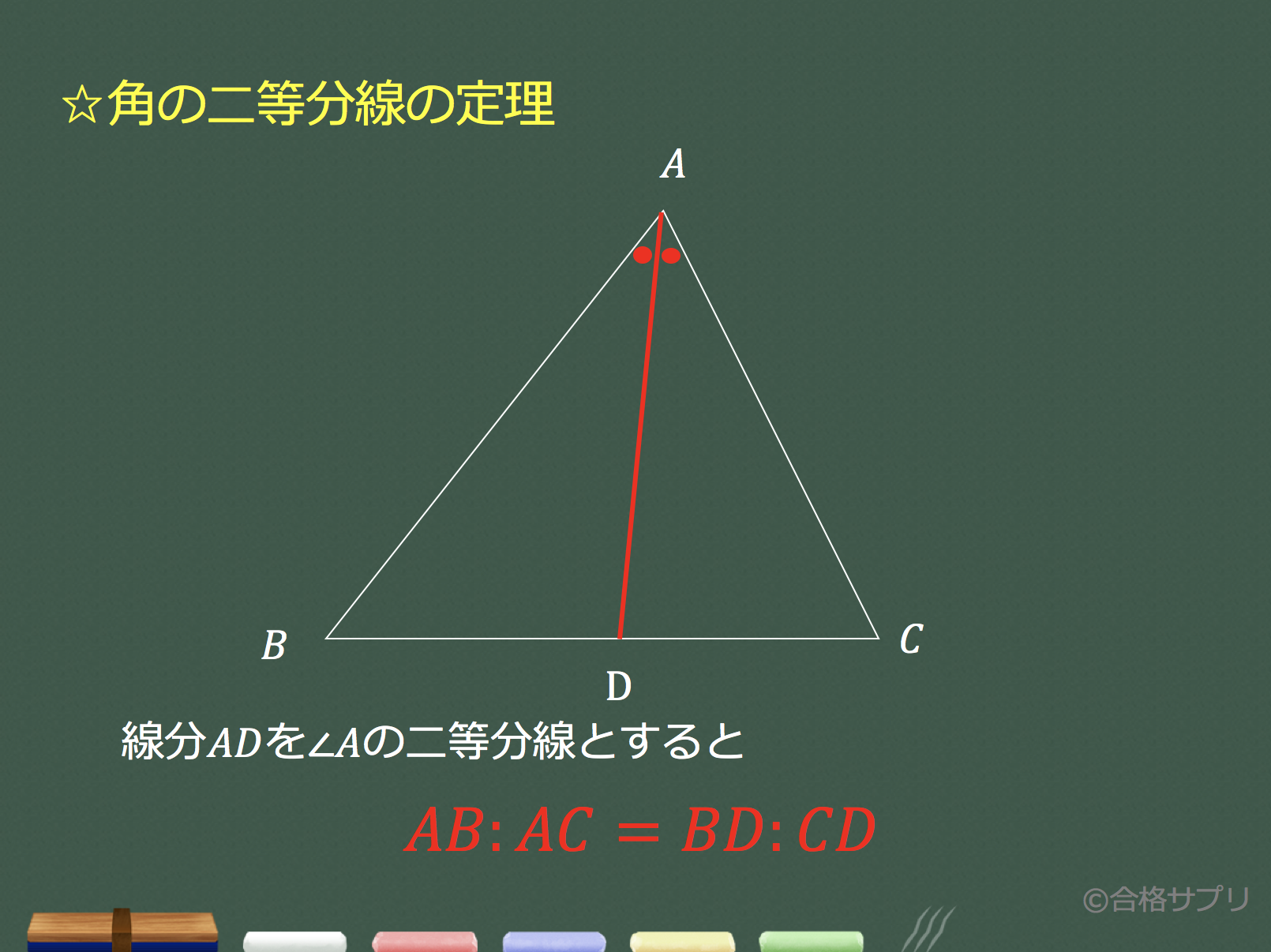
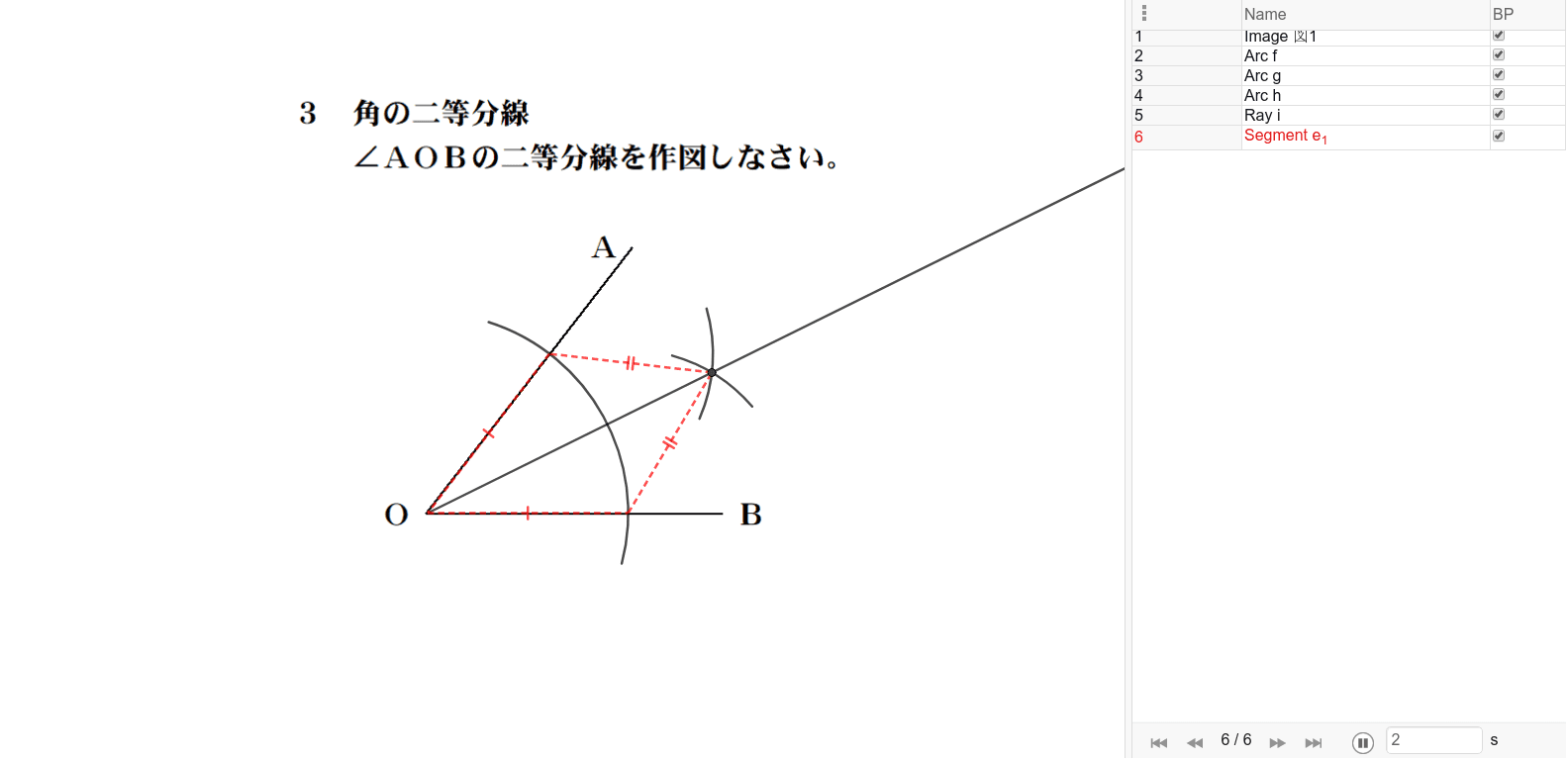
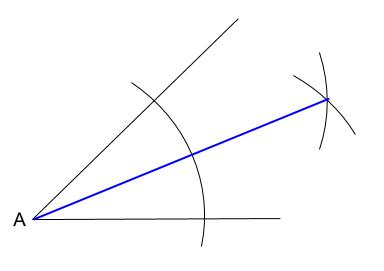
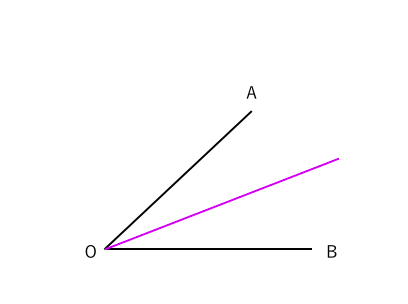
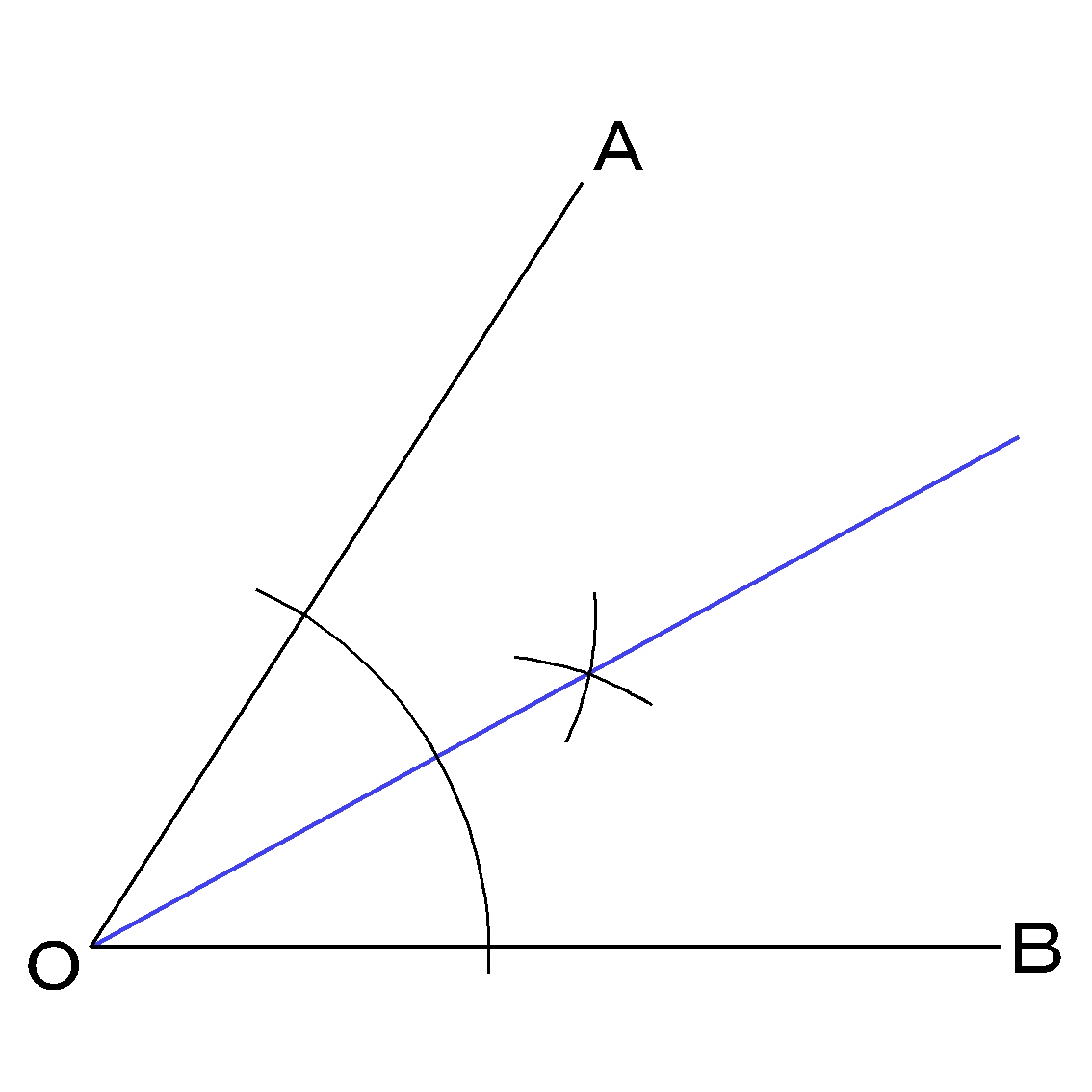
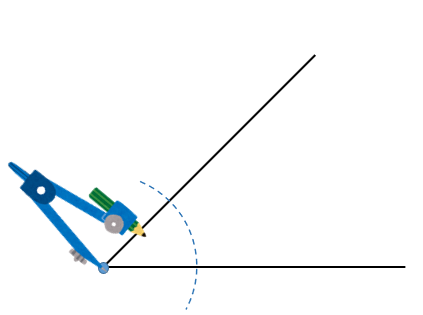
三角形 二等分線 書き方- 三角形の角の二等分線の長さ 頑張って計算するとこんな感じ 三角形の角の二等分線の長さ 赤字の部分に注目しましょう。 三角形の角の二等分線の長さ ここで登場するのが、 最初に作った関係式です。 それぞれを置き換えると このようにAD^2=の式角の二等分線・作図 3 ステップ 1 、 ∠ O を中心に円を書き、交点を P 、 Q とする 2 、 P と Q を中心に円を書き、交点を R とする 3 、 O と R を通る直線を書く 1 ステップずつ、角の二等分線の作図を見ていきましょう。 角の二等分線を作図する問題 まず

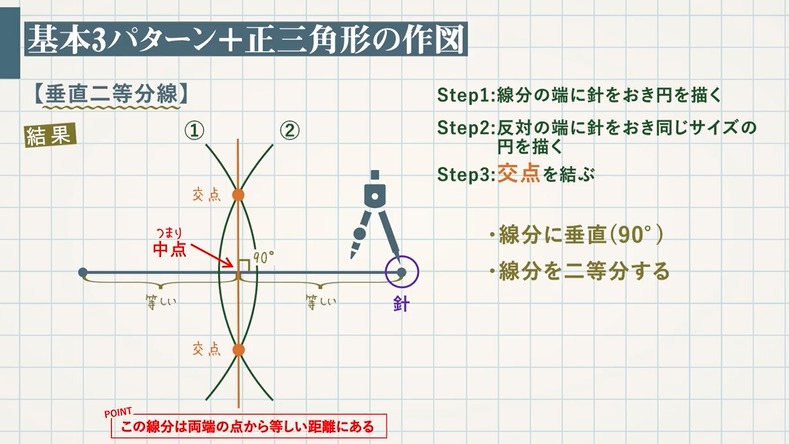
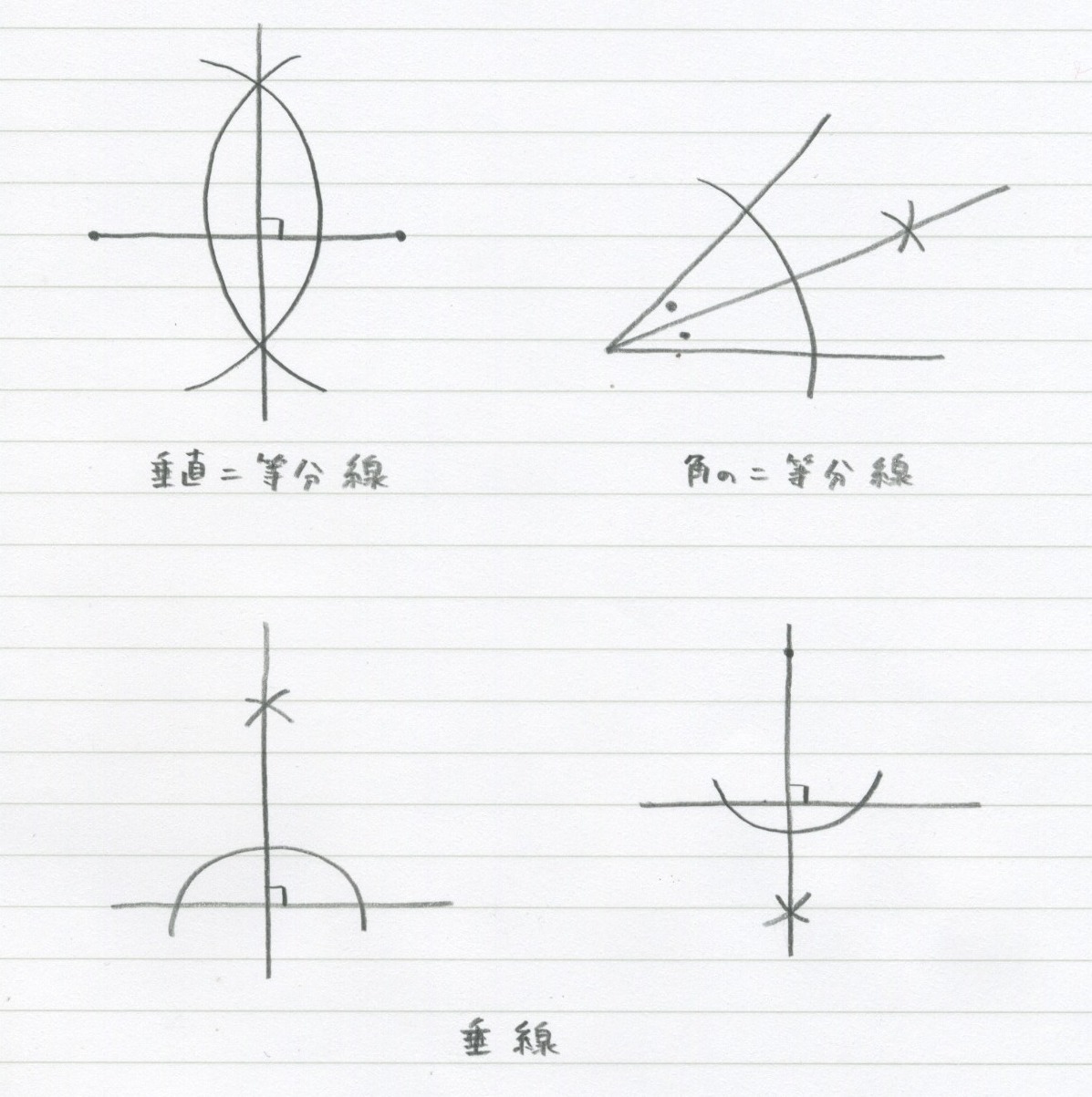
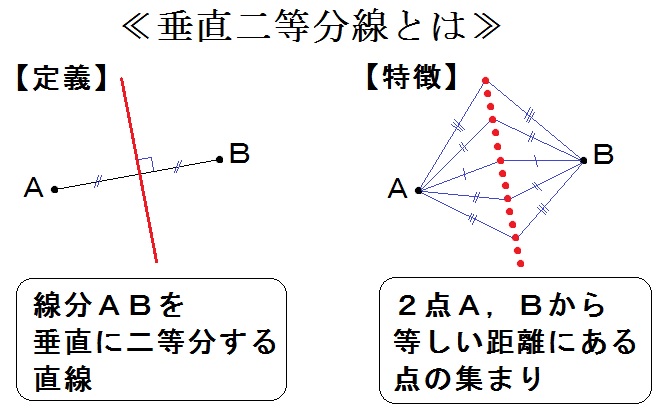
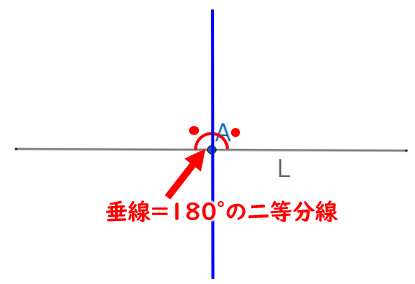
垂直二等分線の作図方法 書き方 と なぜ正しいのか 証明をわかりやすく解説 垂線 遊ぶ数学
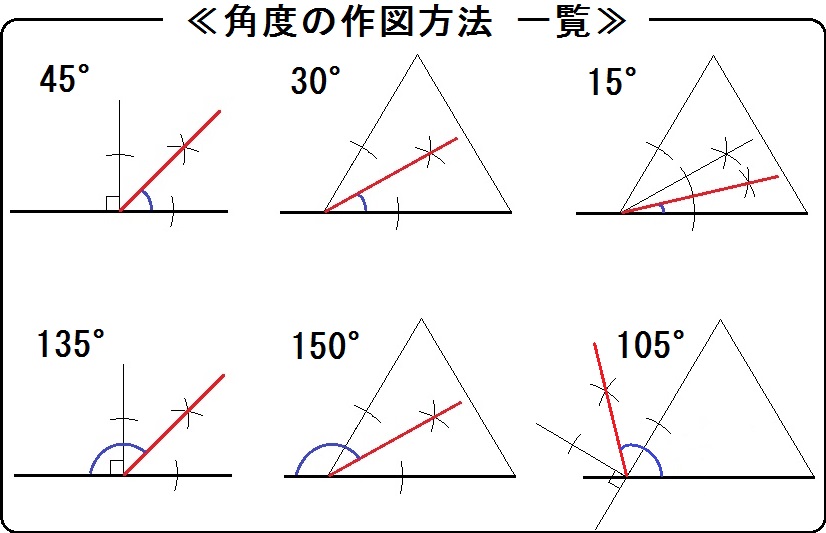
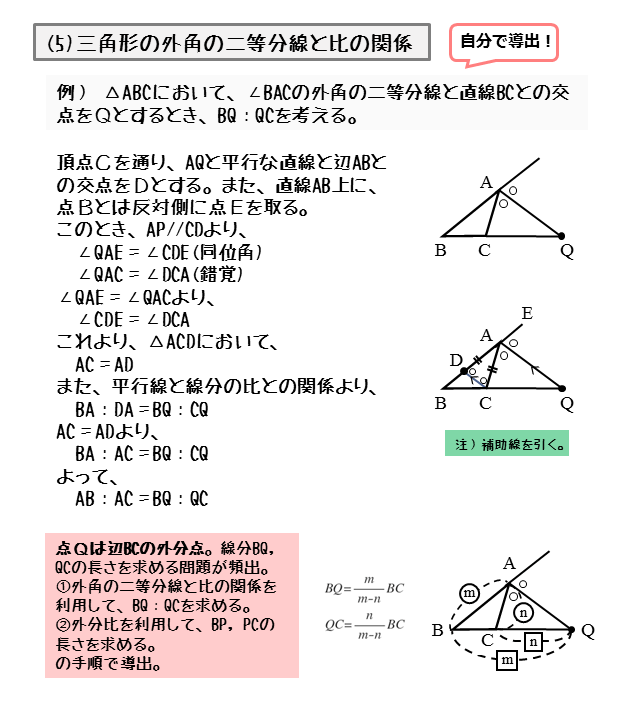
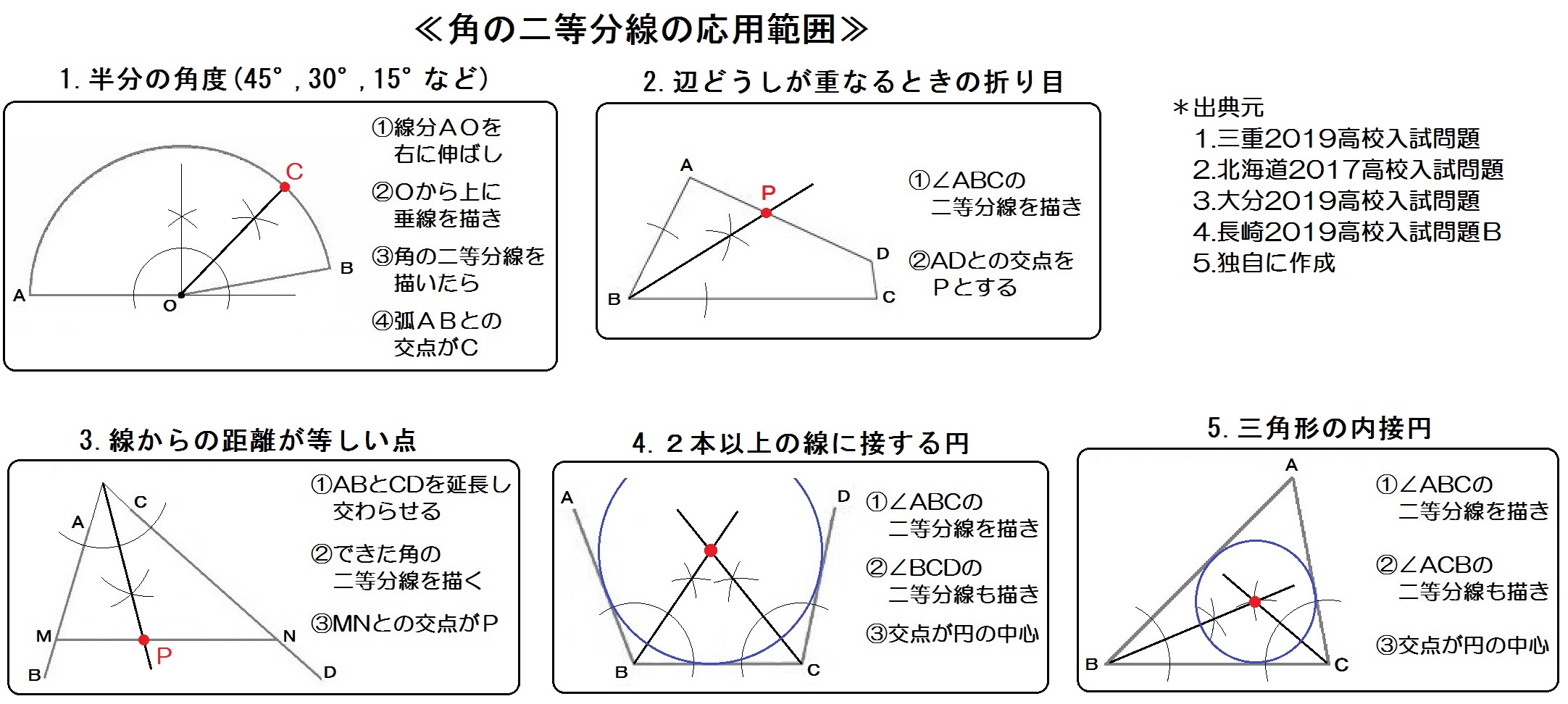
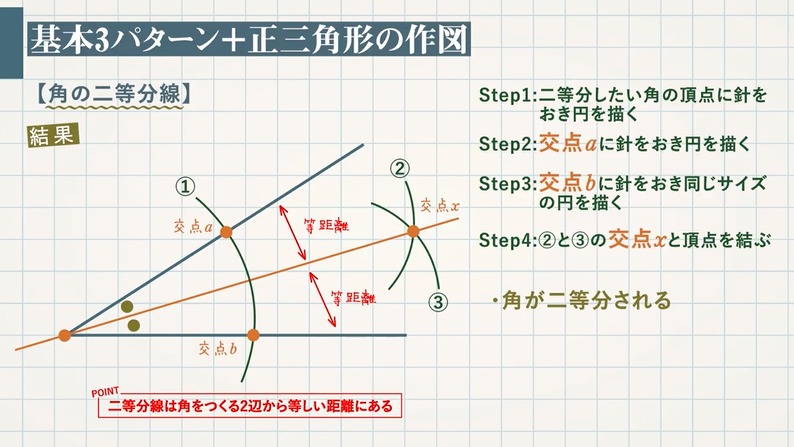
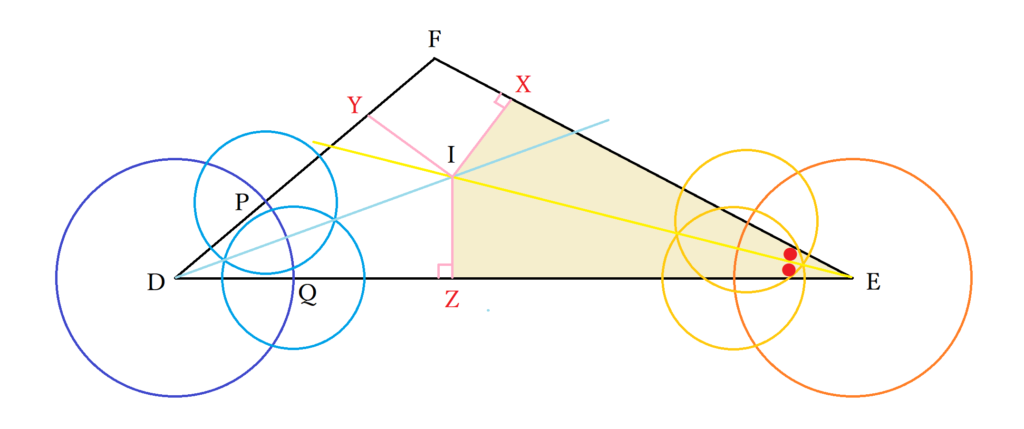
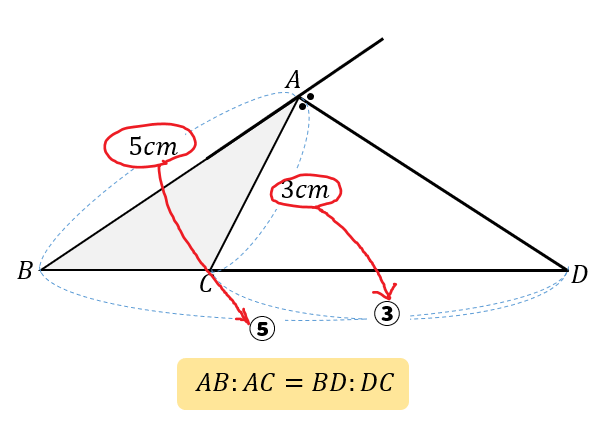
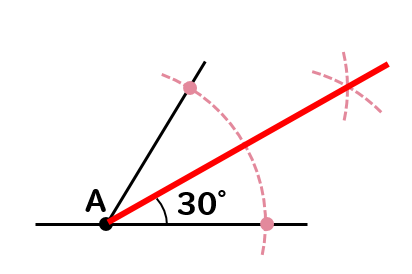
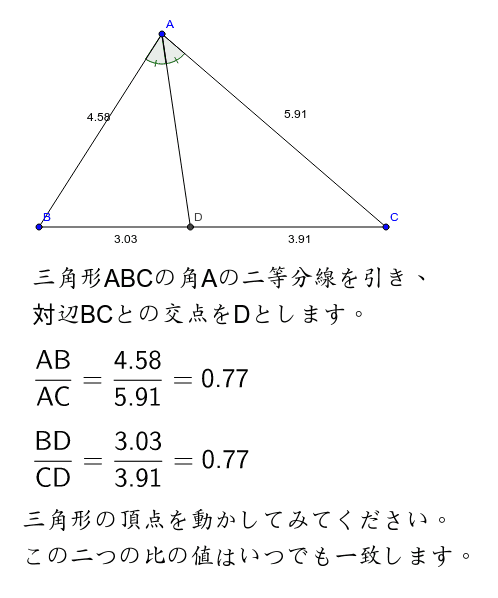
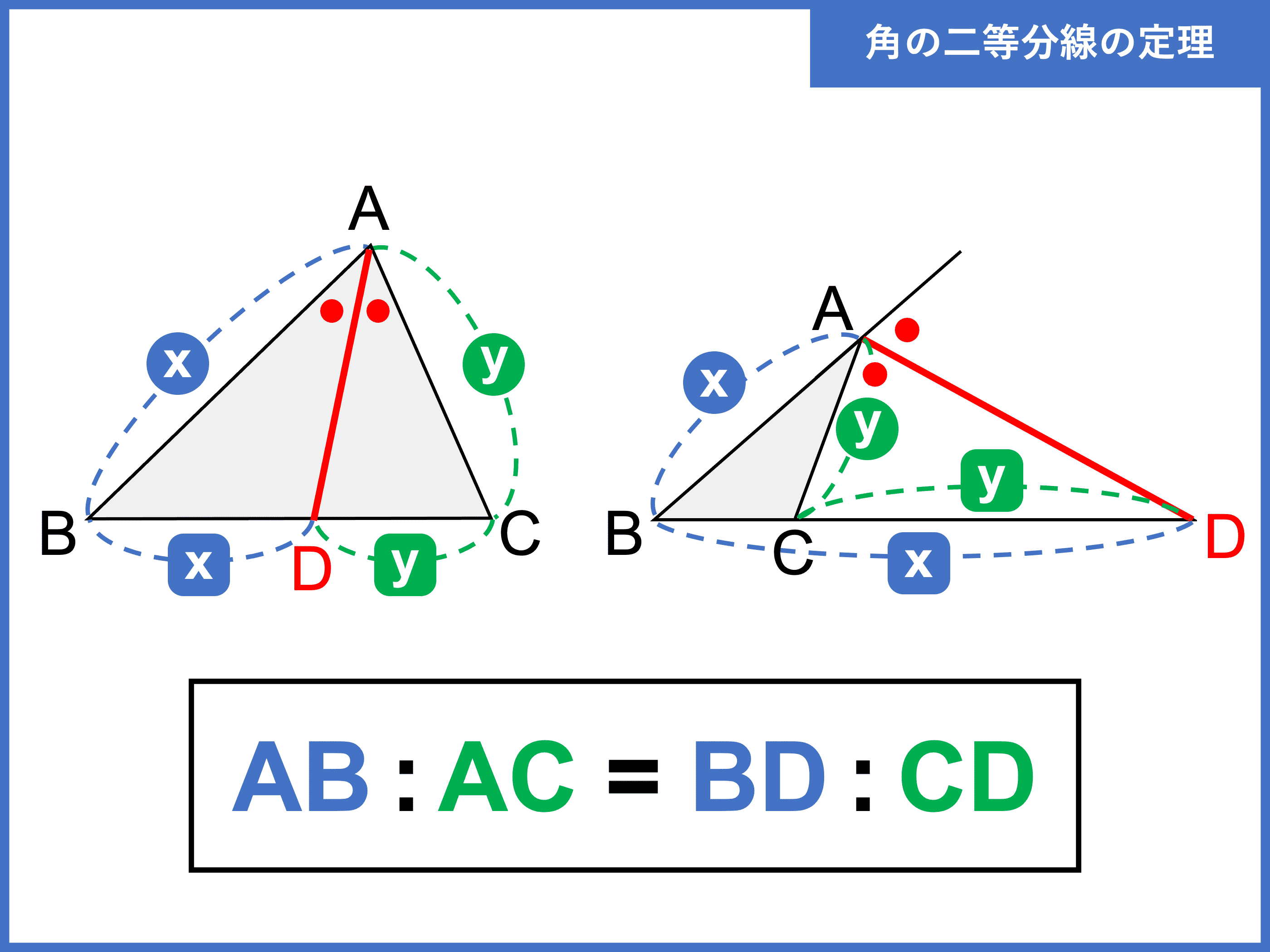
\(30°\) といえば、\(60°\) の二等分なのです。 では、\(60°\) と言えば? そうです。 正三角形の内角です。 つまり 正三角形の作図で、\(60°\) をつくる \(60°\) を二等分する; おわりに ここでは、角の二等分線の簡単な復習と、三角比とからめた問題の例を見ました。 上の例題では、 $\angle \mathrm{ A }=1^{\circ}$ となっていて、この三角比も、半分の角の三角比も、両方とも具体的に値を求めることができるため、上のような解き方ができます。とし,BCとの交点をPとすると PB:PC=AB:AC である. 証明 頂点B,頂点Cから二等分線 ℓ
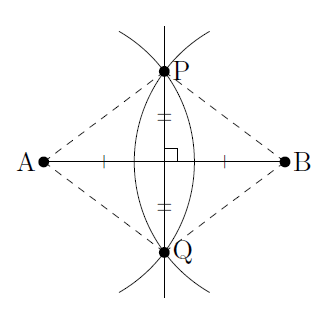
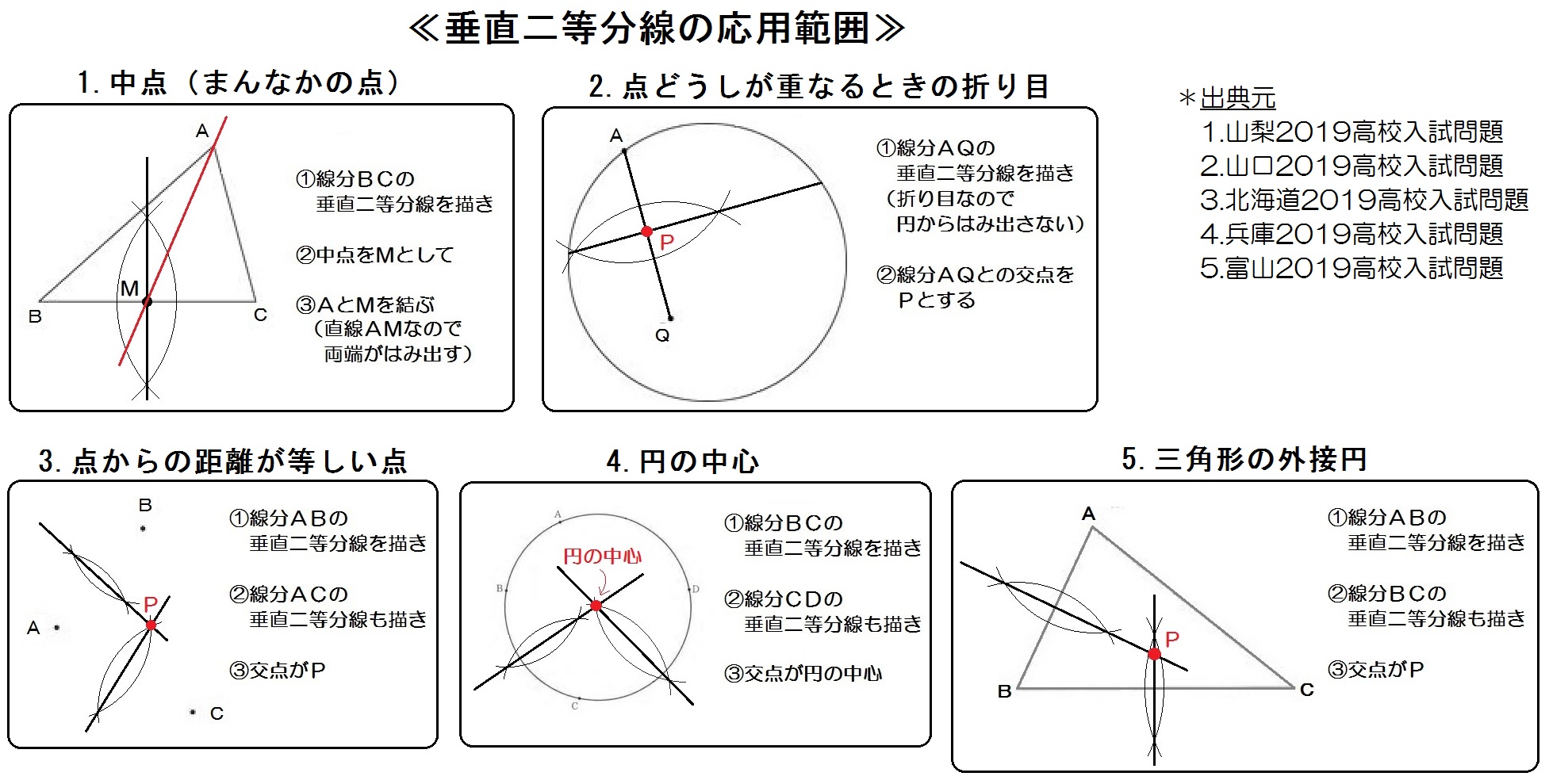
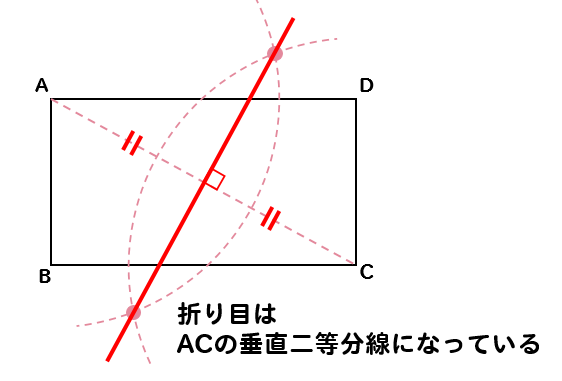
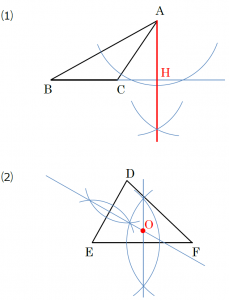
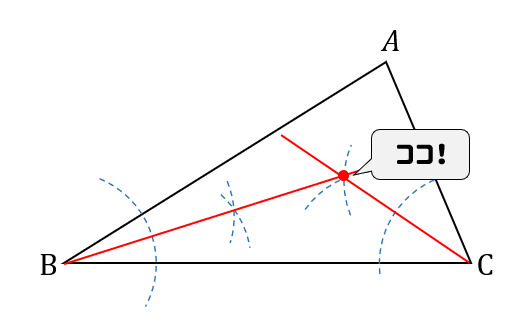
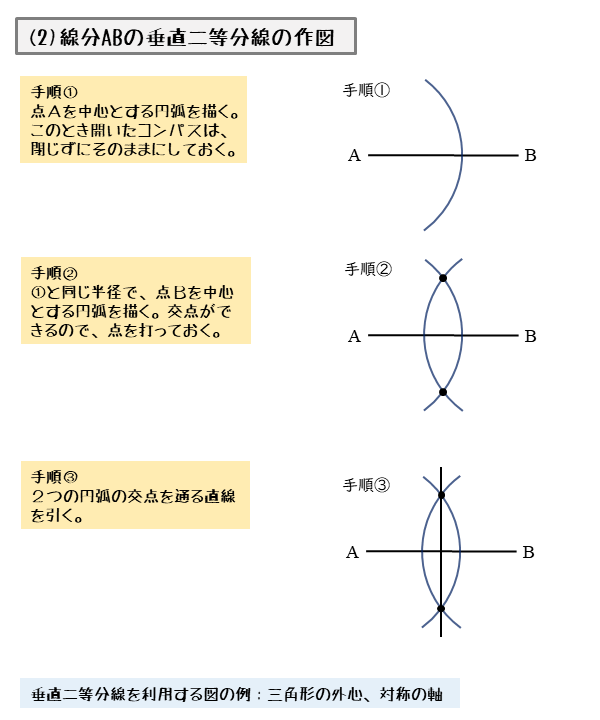
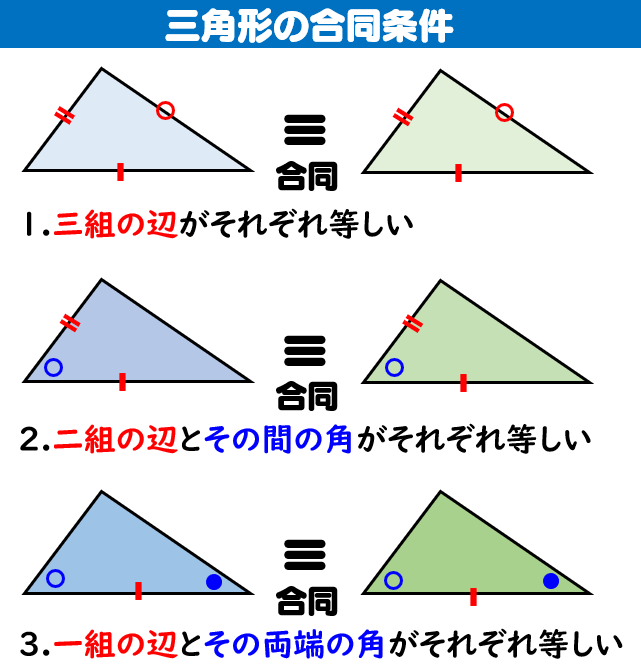
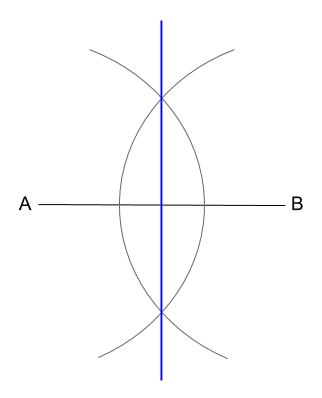
では、なぜこのように描いた線が角の二等分線になるのか解説していきます。 角の二等分線になる理由を解説 これをきちんと証明するには中学校2年生で習う 「三角形の合同条件」 の知識が必要ですが、習っていなくても説明すれば一応は理解して1 二等分 作図:角を二等分する 1 点o を中心とし、適当な半径の円⃝1 を描く。 2 円⃝1 と辺oaとの交点をo1 とする。 3 円⃝1 と辺ob との交点をo2 とする。 4 o1 を中心とし、適当な半径の円⃝2 を描く。 5 o2 を中心とし、円⃝2 の半径と同じ半径の円⃝3 を描く。 6 円⃝2 と円⃝3 の交点をgとする。 交点を結ぶと垂直二等分線が引ける。 垂直二等分線とabの交点からabどちらの点までと同じ長さ(交点a,交点bは同じ長さになっているはず)の印を、 垂直二等分線上にコンパスで付ける、上下どちらでもok。 その印とa、印とbを結ぶと直角二等辺三角形が
三角形 二等分線 書き方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
「三角形 二等分線 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「三角形 二等分線 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「三角形 二等分線 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「三角形 二等分線 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「三角形 二等分線 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「三角形 二等分線 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三角形 二等分線 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「三角形 二等分線 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「三角形 二等分線 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「三角形 二等分線 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「三角形 二等分線 書き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |
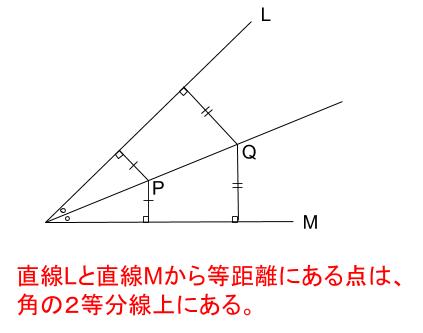
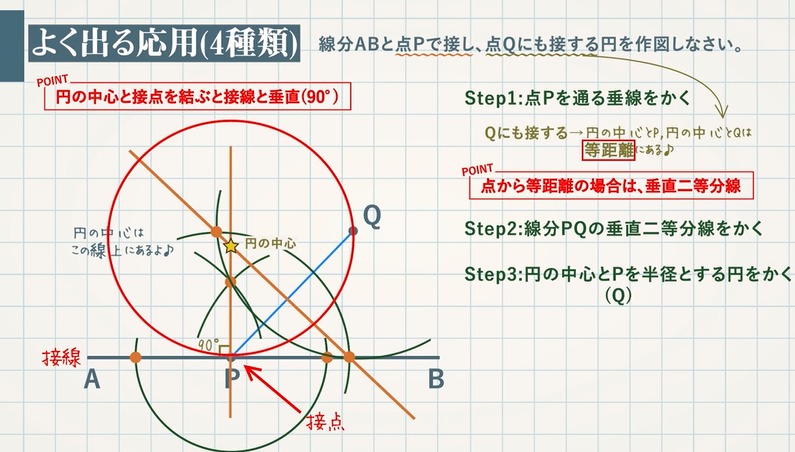
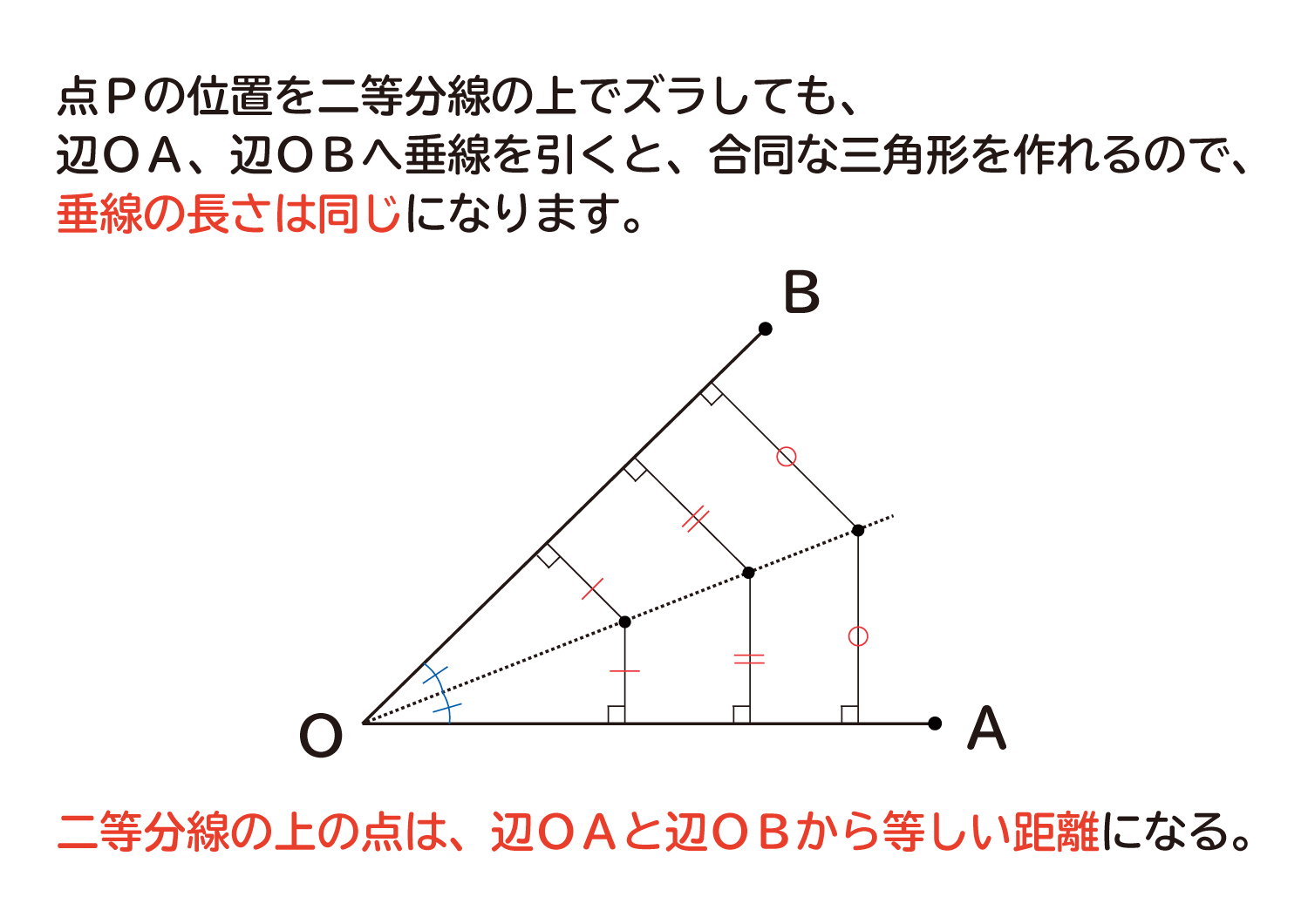
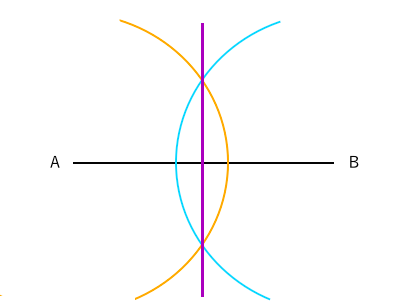
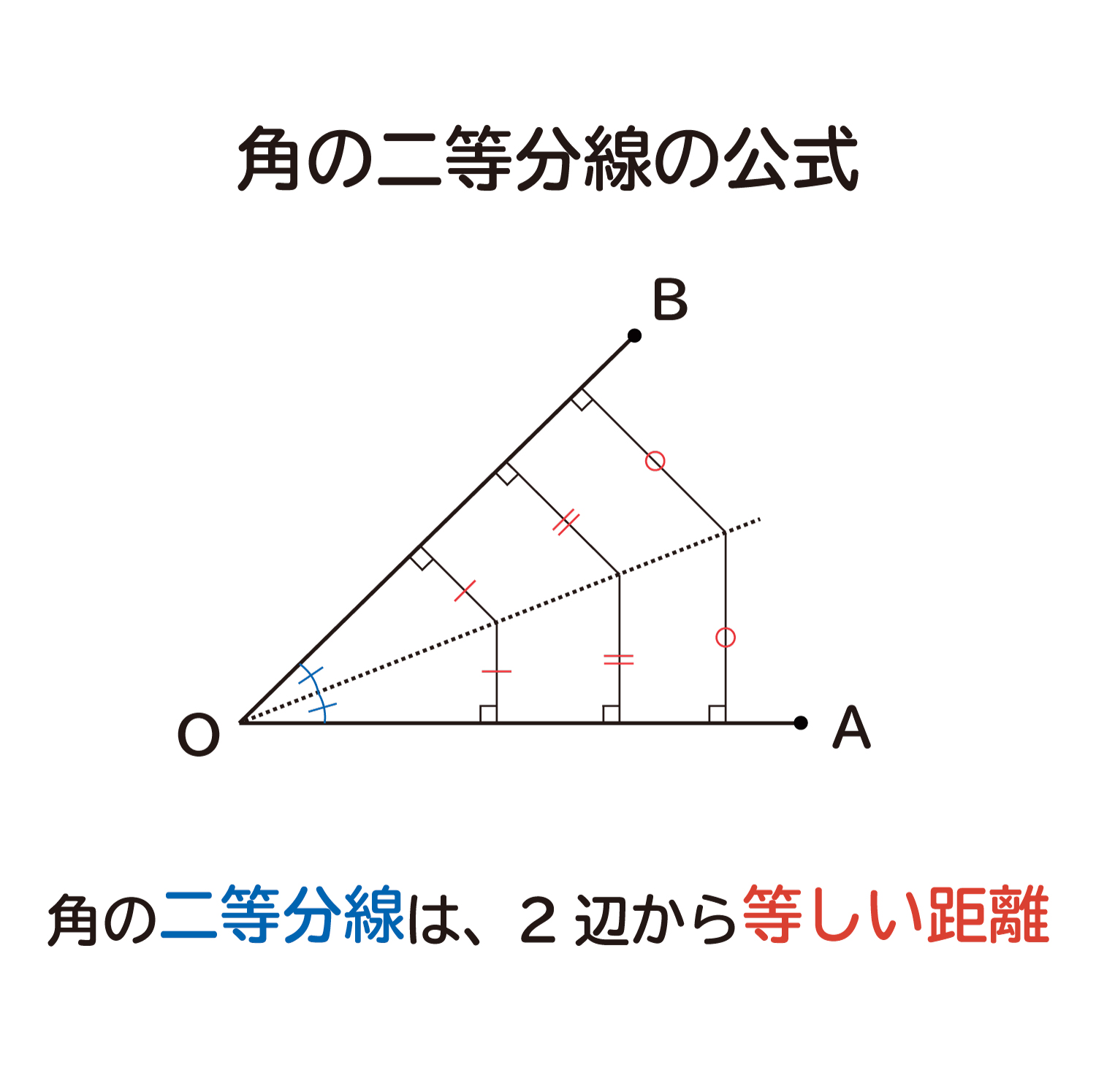
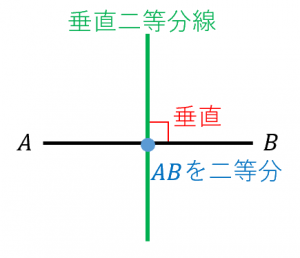
角の二等分線は、 2 2 つの直線から等距離にある点の集合です。 単純に、「 2 2 辺からの距離が等しい直線は角の二等分線」ともいいます。 垂直二等分線の作図と角の二等分線の作図。 必ず暗記しましょう。 これがすべての作図に通ずる超重要事項です以上が垂直二等分線の書き方ですが、「なぜこれが垂直二等分線になるのか」についても解説していきます。 垂直二等分線になる理由 まず、ふたつの弧が交わる点について考えてみましょう。 これらはどういった点なのでしょうか?
Incoming Term: 三角形 二等分線 書き方,
コメント
コメントを投稿